ENGINEERING FOUNDATION YEAR MECHANIC 2 EXPERIMENTS

Introduction

The aim of this experiment is to evaluate the linear speed on a glider in motion. The aspect of the glider’s acceleration will also be evaluated. The force applied to the glider from the review of a free body depiction of the system in motion will be conducted. The application of Newton’s Second law of motion in order to ascertain the weight of the glider will be implemented. The intensity of any frictional forces on the moving system of the glider will also be applied.

Materials

1. An aeration propelled track with one of the stationary mass card gliders suspended on a track of eleven centimeters in longitude,
2. Collection of weights which possess slots having a comprehensive mass of 24.9 Gms.
3. Metric measurement stick
4. Dual photo gates
5. Blower
6. Attachment cord.
7. Pulley

Procedure

1. The machinery was set up as demonstrated in the diagram. The photo gates which were connected to the dual chronometer had been established in a manner where the glider passes through the dual beams of light which are located on the opposite ends of the aerated track.
2. The aspect of the level of the horizontal aerated track had been reviewed. The photo gates were established at a separation of 0.7 m one was positioned at 1.3 m and the other had been positioned at 0. 6 m of the longitude of the aerated track.
3. A hanging weight which possessed a mass equivalent to 5.04 Gms was attached to the line. The additional four weights had been placed on the glider which was situated on the aerated track. The weights were placed in the shallow aspect of the card glider. The glider had been positioned at the mark which was evaluated at 1.4 m on the aerated track which was 0.1 m of a distanced from the initial photo gate. The glider had been maintained in position. The blower which generated the cushion of air was established at a moderate setting. The indicator was positioned at the 11 o’ clock setting.
4. The mode of the chronometer was established at photo gate. The time which lapsed for the movement of the card which had been positioned on the aerated glider was documented as the glider crossed each of the light beams.
5. The glider was slightly released from a resting position. The two temporal intervals which were required for the aerated glider to pass by each of the photo gates were documented.
6. The test had been repeated three times and a mean time was derived for the glider to pass by each of the photo gates.
7. One of the masses was taken off the glider and paced upon n the hanging weight. The comprehensive mass which was attached to the glider had been added to the mass which was held in suspension from the cord. The temporal interval which lapsed for the aerated glider card to pass by each of the photo gates which are t₁ and t₂ had been documented.

1. The steps which had been applied from 4- 7 were repeated until the comprehensive suspended mass attained a weight of 24.7 g.
2. The distance of the longitude of the card on the aerated track had been evaluated. The distance which separated the photo gates had also been reevaluated.
3. The outcomes were documented on a table. In the circumstance of each of the masses which were suspended the formulas of the application of kinematic equations in order to compute the acceleration had been applied. This aspect is assessed in m/ s². Subsequently the intensity of the forces which had been applied for each assessed wright of the suspended weight by the application of FBD review and the assessed values was conducted.
4. A graph demonstrating the applied forces in comparison to the acceleration was made.
5. The mass of the glider was ascertained from the information which was depicted graphically and the origins of any uncertainties were detailed.

Theory

Consequent to the theories which had been reviewed in the coursework, distinct free body diagrams for the suspended weight which is m_s and the comprehensive mass in motion mtotal was drawn. It should be noted that the weight of the aerated glider and the total of the suspended weights would be depicted as M_total = m_s + M_glider. In the transference of the weights from the aerated trolley to the suspended weight, the comprehensive mass of the system is being consistently maintained. The aspect of the experiment enabled the ascertaining of the force which was applied. This force is equal to the force which was exerted upon the suspended chord. This force is the equivalent force which is supplied for the acceleration to the comprehensive mass in motion. Conducting an equalization of these forces will facilitate the computation of the mass which is in movement, the comprehensive mass of the system and the real mass of the glider m_glider.

Table One Applied Force vs. Acceleration

Trial	Velocity m/ s	Acceleration ( m/ s2 )	Distance (m)	Force (N) 0.00504 kg	Force (N) 0.01334 kg	Force (N) 0.02164 kg	Force (N) 0.02994 kg
1	15.08	0	0.20	0.04932	0.130732	0.212072	0.293412
2	15.55	0.43	0.20	0.04932	0.130732	0.212072	0.293412
3	15.2	– 0.35	0.20	0.04932	0.130732	0.212072	0.293412
4	13.8	– 1.4	0.24	0.04932	0.130732	0.212072	0.293412
5	13.9	0.1	0.24	0.04932	0.130732	0.212072	0.293412
6	13.92	0.02	0.24	0.04932	0.130732	0.212072	0.293412
7	12.15	– 0.83	0.32	0.04932	0.130732	0.212072	0.293412
8	12.1	– 0.05	0.32	0.04932	0.130732	0.212072	0.293412
9	12.16	– 0.06	0.32	0.04932	0.130732	0.212072	0.293412

 

Sample size: 9
Mean x (x?): 0.36
Mean y (y?): 0.25333333333333
Intercept (a): 0.25317390020667
Slope (b): 0.00044286979627991
Regression line equation: y=0.25317390020667+0.00044286979627991x

 

Height ( m)	Distance (m)	Time (s)	Velocity (m/s)	Acceleration m/s2	Force (N) 0.01334 kg	Force (N) 0.02164 kg	Force (N) 0.02994 kg
0.024	0.64	0.4525	0.64/0.4525= 1.4143	0	0.130732	0.212072	0.293412
0.026	0.64	0.450	1.42	0.0036	0.130732	0.212072	0.293412
0.032	0.82	0.648	1.256	-.164	0.130732	0.212072	0.293412

Sample size: 5
Mean x (x?): 0.03352
Mean y (y?): 0.1272432
Intercept (a): 0.084319096954357
Slope (b): 1.2805520001683
Regression line equation: y=0.084319096954357+1.2805520001683x

Experiment Two Rotations of a Flywheel

Objectives

The objectives of this laboratory experiment are: To evaluate the angular and radial acceleration qualities of a steel flywheel. To determine the inertial moment of the steel flywheel. The objective is to ascertain the weight of the flywheel. The objectives are to calculate any qualities of frictional torque which are exerted upon the flywheel axle as it experiences acceleration from a mass which is falling.

Materials

1. Steel flywheel with a 0.22 m radius which is mounted on a horizontal shaft.
2. Hanging weight of approximately 10 N
3. Additional 10 N weights.
4. Chronometer
5. Two meter measuring stick.
6. The diameter of the steel flywheel and the radius of 0.022 m which is exerted on the axle rod.

Methods

1. Envelope one of the extremes of the cord around the circumference of the axle rod.
2. Secure the hanging weight 10 N to an opposite end of the cord in order that the inferior aspect of the hanging weight is at a height of two meters from the floor.
3. Free the hanging weight and evaluate the time that it takes to touch the floor.
4. Repeat steps one – three with supplemental weights attached to the hanging weight
5. In each of the trials compute the lineal acceleration of the weights with the formula 2S/ t2 = a. Derive the angular and radial acceleration of the axle rod and the steel flywheel with the formula rad/ s² = ?. This is considering that the radius of the axle from which the rope is wrapped is equival8ient to 0.022 m.
6. In each of the trials compute the torque which is derived from the mass applied to the axle rod.
7. Demonstrate as graph of torque (t) verse angular and radial acceleration and calculate the intercept and the slope of the equation
8. As an outcome of the graphical value of t (slope) approximate the mass of the flywheel.

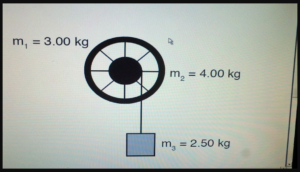
Theory

The torque which is exerted upon the suspended weight F (N) on the axle rod Fr (Nm) = T.  In order to calculate the net torque which is exerted upon the steel flywheel the formula which is applied is I?, considering that I?, = T – T_f in the circumstance where the torque of the steel flywheel is equal to I? + T_f. The frictional resistance which is represented by the steel flywheel upon the axle is represented by T_f.

Table Two Torque vs. Acceleration

Force Applied (N)	Elapsed Time (s)	Torque (Nm)	Angular acceleration (rad/ s2)	Lineal acceleration (m/s2)
10	25	0.22	0	0
20	17	0.44	0.0275	0.01375
30	14	0.66	0.073	0.0365
40	11	0.88	0.073	0.0365
50	10	1.1	0.099	0.04545
60	9	1.32	0.476	0.238
70	8	1.54	0.476	0.238

Sample size: 7
Mean x (x?): 0.88
Mean y (y?): 0.17492857142857
Intercept (a): -0.16092857142857
Slope (b): 0.38165584415584
Regression line equation: y=0.38165584415584x-0.16092857142857, weight of steel flywheel is 0.1609 kg.

Follow the link to learn more about How Many Sentences Are in a Paragraph?